树

简介

树是一种数据结构，由n个有限节点组成的一个具有层次关系的集合。二叉树则是每个节点最多有两个子树的树结构。二叉树一般有以下性质：

二叉树第k层上的节点数目最多为 $2^{k-1}$
深度为 h 的二叉树至多有 $2^{h-1}$ 个节点。
包含 n 个节点的二叉树的高度至少为 $log_2(n+1)$
在任意一棵二叉树中，若叶子节点的个数为 $n_0$ ，度为2的节点数为 $n_2$ ，则 $n_0 = n_2 + 1$

常见相关术语

根节点（root node）：位于二叉树顶层的节点，没有父节点
叶节点（leaf node）：没有子节点的节点
边（edge）：连接两个节点的线段
节点所在的层（level）：从顶至底递增，根节点所在层为1
节点的度（degree）：节点的子节点数量。在二叉树中，度的取值范围为0、1、2
二叉树的高度（height）：从根节点到最远叶节点所经过的边的数量
节点的深度（depth）：从根节点到该节点所经过的边的数量
节点的高度（height）：从距离该节点最远的叶节点到该节点所经过的边的数量。

常见的二叉树

完美二叉树（Perfect binary tree），也叫满二叉树。如果一棵二叉树的节点要么是叶子节点，要么它有两个子节点，那么这样的树就是完美二叉树。

完全二叉树（Complete binary tree）。完全二叉树（complete binary tree）只有最底层的节点未被填满，且最底层节点尽量靠左填充。请注意，完美二叉树也是一棵完全二叉树。（PS: mermaid绘图，叶子节点可能比较奇怪）

平衡二叉树（balanced binary tree）。一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

二叉搜索树。若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值。

实现二叉树

Python

class TreeNode:
    """二叉树节点类"""
    def __init__(self, val: int):
        self.val: int = val                # 节点值
        self.left: TreeNode | None = None  # 左子节点引用
        self.right: TreeNode | None = None # 右子节点引用

if __name__ == '__main__':
    # 初始化二叉树
    # 初始化节点
    n1 = TreeNode(val=1)
    n2 = TreeNode(val=2)
    n3 = TreeNode(val=3)
    n4 = TreeNode(val=4)
    n5 = TreeNode(val=5)
    # 构建节点之间的引用（指针）
    n1.left = n2
    n1.right = n3
    n2.left = n4
    n2.right = n5
    
    # 插入与删除节点
    p = TreeNode(0)
    # 在 n1 -> n2 中间插入节点 P
    n1.left = p
    p.left = n2
    # 删除节点 P
    n1.left = n2

遍历二叉树

从物理结构的角度来看，树是一种基于链表的数据结构，因此其遍历方式是通过指针逐个访问节点。然而，树是一种非线性数据结构，这使得遍历树比遍历链表更加复杂，需要借助搜索算法来实现。

二叉树常见的遍历方式包括层序遍历、前序遍历、中序遍历和后序遍历等。

层序遍历

层序遍历（level-order traversal）从顶部到底部逐层遍历二叉树，并在每一层按照从左到右的顺序访问节点。层序遍历本质上属于广度优先遍历（breadth-first traversal），也称广度优先搜索（breadth-first search, BFS），它体现了一种“一圈一圈向外扩展”的逐层遍历方式。

广度优先遍历通常借助“队列”来实现。队列遵循“先进先出”的规则，而广度优先遍历则遵循“逐层推进”的规则，两者背后的思想是一致的。

# Python实现层序遍历
def level_order(root: TreeNode | None) -> list[int]:
    """层序遍历"""
    # 初始化队列，加入根节点
    queue: deque[TreeNode] = deque()
    queue.append(root)
    # 初始化一个列表，用于保存遍历序列
    res = []
    while queue:
        node: TreeNode = queue.popleft()  # 队列出队
        res.append(node.val)  # 保存节点值
        if node.left is not None:
            queue.append(node.left)  # 左子节点入队
        if node.right is not None:
            queue.append(node.right)  # 右子节点入队
    return res

前序、中序、后序遍历

前序、中序和后序遍历都属于深度优先遍历（depth-first traversal），也称深度优先搜索（depth-first search, DFS），它体现了一种“先走到尽头，再回溯继续”的遍历方式。

深度优先搜索通常基于递归实现。

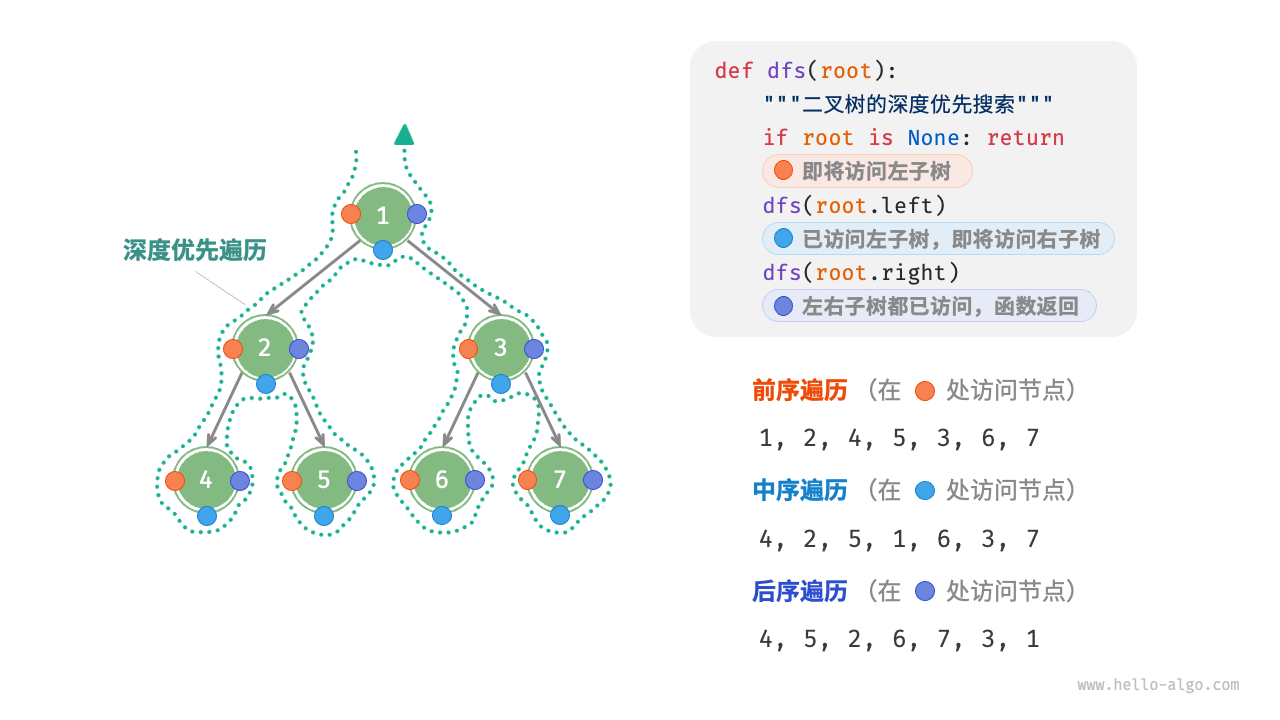
binary_tree_dfs

代码实现

# Python深度优先遍历二叉树
class TreeNode:
    """二叉树节点类"""
    def __init__(self, val: int):
        self.val: int = val                # 节点值
        self.left: TreeNode | None = None  # 左子节点引用
        self.right: TreeNode | None = None # 右子节点引用

def list_to_tree_dfs(arr: list[int], i: int) -> TreeNode | None:
    """将列表反序列化为二叉树：递归"""
    # 如果索引超出数组长度，或者对应的元素为 None ，则返回 None
    if i < 0 or i >= len(arr) or arr[i] is None:
        return None
    # 构建当前节点
    root = TreeNode(arr[i])
    # 递归构建左右子树
    root.left = list_to_tree_dfs(arr, 2 * i + 1)
    root.right = list_to_tree_dfs(arr, 2 * i + 2)
    return root

def list_to_tree(arr: list[int]) -> TreeNode | None:
    """将列表反序列化为二叉树"""
    return list_to_tree_dfs(arr, 0)


def pre_order(root: TreeNode | None):
    """前序遍历"""
    if root is None:
        return
    # 访问优先级：根节点 -> 左子树 -> 右子树
    res.append(root.val)
    pre_order(root=root.left)
    pre_order(root=root.right)

def in_order(root: TreeNode | None):
    """中序遍历"""
    if root is None:
        return
    # 访问优先级：左子树 -> 根节点 -> 右子树
    in_order(root=root.left)
    res.append(root.val)
    in_order(root=root.right)

def post_order(root: TreeNode | None):
    """后序遍历"""
    if root is None:
        return
    # 访问优先级：左子树 -> 右子树 -> 根节点
    post_order(root=root.left)
    post_order(root=root.right)
    res.append(root.val)

"""Driver Code"""
if __name__ == "__main__":
    # 初始化二叉树
    # 这里借助了一个从数组直接生成二叉树的函数
    root = list_to_tree(arr=[1, 2, 3, 4, 5, 6, 7])

    # 前序遍历
    res = []
    pre_order(root)
    print("\n前序遍历的节点打印序列 = ", res)

    # 中序遍历
    res.clear()
    in_order(root)
    print("\n中序遍历的节点打印序列 = ", res)

    # 后序遍历
    res.clear()
    post_order(root)
    print("\n后序遍历的节点打印序列 = ", res)

二叉搜索树

二叉搜索树（binary search tree）满足以下条件。

对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
任意节点的左、右子树也是二叉搜索树，即同样满足条件 1. 。

常见操作

二叉搜索树的查找操作与二分查找算法的工作原理一致，都是每轮排除一半情况。循环次数最多为二叉树的高度，当二叉树平衡时，使用 O(log⁡n) 时间

class TreeNode:
    """二叉树节点类"""
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None


class BinarySearchTree:
    """二叉搜索树"""

    def __init__(self):
        """构造方法"""
        # 初始化空树
        self._root = None

    def search(self, num: int) -> TreeNode | None:
        """查找节点"""
        cur = self._root
        # 循环查找，越过叶节点后跳出
        while cur is not None:
            # 目标节点在 cur 的右子树中
            if cur.val < num:
                cur = cur.right
            # 目标节点在 cur 的左子树中
            elif cur.val > num:
                cur = cur.left
            # 找到目标节点，跳出循环
            else:
                break
        return cur

    def insert(self, num: int):
        """插入节点"""
        # 若树为空，则初始化根节点
        if self._root is None:
            self._root = TreeNode(num)
            return
        # 循环查找，越过叶节点后跳出
        cur, pre = self._root, None
        while cur is not None:
            # 找到重复节点，直接返回
            if cur.val == num:
                return
            pre = cur
            # 插入位置在 cur 的右子树中
            if cur.val < num:
                cur = cur.right
            # 插入位置在 cur 的左子树中
            else:
                cur = cur.left
        # 插入节点
        node = TreeNode(num)
        if pre.val < num:
            pre.right = node
        else:
            pre.left = node


"""Driver Code"""
if __name__ == "__main__":
    # 初始化二叉搜索树
    bst = BinarySearchTree()
    nums = [4, 2, 6, 1, 3, 5, 7]
    for num in nums:
        bst.insert(num)

    # 查找节点
    node = bst.search(7)
    print("\n查找到的节点对象为: {}，节点值 = {}".format(node, node.val))

AVL树

nil

简介​

常见相关术语​

常见的二叉树​

实现二叉树​

Python​

遍历二叉树​

层序遍历​

前序、中序、后序遍历​

二叉搜索树​

常见操作​

AVL树​

简介